pvigier's blog
computer science, programming and other ideas
Fractal Image Compression
One year ago, I coded a very simple implementation of fractal image compression for a course and I made the code available on github there.
To my surprise, the repo is quite popular. So I decided to update the code and to write an article to explain the theory and the code.
Theory
This part is quite technical, you can skip it if you are only interested by a documentation of the code.
Contractions
Let \((E, d)\) be a complete metric space and \(f : E \rightarrow E\) a mapping from \(E\) to \(E\).
We will say that \(f\) is a contraction if there exists \(0 < s < 1\) such that:
\[\forall x, y \in E, d(f(x), f(y)) \leq sd(x, y)\]From here, \(f\) will denote a contraction with contractivity factor \(s\).
There are two important theorems on contractions: the Contraction Mapping Theorem and the Collage Theorem.
Theorem (Contraction Mapping Theorem): \(f\) has an unique fixed point \(x_0\).
First, let us proof that the sequence \((u_n)\) defined by \(\left\{\begin{alignat*}{2}u_0 & = x\\ u_{n+1} & = f(u_n)\end{alignat*}\right.\) is convergent for all \(x \in E\).
For all \(m < n \in \mathbb{N}\):
$$ \begin{alignat*}{2} d(u_m, u_n) & = d(f^m(x), f^n(x)) \\ & \leq s^md(x, f^{n-m}(x)) \text{ because } f \text{ is a contraction} \\ & \leq s^m\left(\sum_{i=0}^{n-m-1}{d(f^i(x), f^{i+1}(x))}\right) \text{ by the triangular inequality} \\ & \leq s^m\left(\sum_{i=0}^{n-m-1}{s^id(x, f(x))}\right) \text{ because } f \text{ is a contraction} \\ & = s^m\left(\frac{1 - s^{n-m}}{1 - s}d(x, f(x))\right) \\ & \leq \frac{s^m}{1 - s}d(x, f(x)) \underset{m \rightarrow \infty}{\rightarrow} 0 \end{alignat*} $$So \((u_n)\) is a Cauchy sequence and as \(E\) is complete, \((u_n)\) is convergent. Let \(x_0\) bet its limit.
Moreover, as a contraction is Lipschitz-continuous, it is also continuous so \(f(u_n) \rightarrow f(x_0)\). Thus, if we let \(n\) tend to infinity in \(u_{n+1} = f(u_n)\), we have that \(x_0 = f(x_0)\). So \(x_0\) is a fixed point of \(f\).
We have shown that \(f\) has a fixed point. Let us show by contradiction that it is unique. Let \(y_0\) be another fixed point, then:
$$ d(x_0, y_0) = d(f(x_0), f(y_0)) \leq sd(x_0, y_0) < d(x_0, y_0) $$Contradiction.
From here, \(x_0\) will denote the fixed point of \(f\).
Theorem (Collage Theorem): If \(d(x, f(x)) < \epsilon\) then \(d(x, x_0) < \frac{\epsilon}{1 - s}\).
We showed in the previous proof that \(d(u_m, u_n) \leq \frac{s^m}{1 - s}d(x, f(x)) = \frac{s^m}{1 - s}\epsilon\).
If we fix \(m\) to \(0\) then we have that \(d(x, u_n) \leq \frac{\epsilon}{1 - s}\).
Finally we let \(n\) tend to infinity to obtain the desired result.
The second theorem tells us that if we find a contraction \(f\) such that \(f(x)\) is near to \(x\) then we are sure that the fixed point of \(f\) is also near to \(x\).
This result will be fundamental in the following. Indeed instead of saving an image, we will only save a contraction whose fixed point is near to the image.
Contractions for Images
In this part, we will show how to build a contraction such that its fixed point is near to a given image.
Firstly, let us define the image set and a distance. We choose \(E = [0, 1]^{h \times w}\). \(E\) is the set of matrices with \(h\) rows, \(w\) columns and with coefficients in \([0, 1]\). Then we take \(d(x, y) = \left(\sum_{i=1}^{h}{\sum_{j=1}^{w}{(x_{ij}-y_{ij})^2}}\right)^{0.5}\). \(d\) is the distance obtained from the Frobenius norm.
Now, let \(x \in E\) the image we want to compress.
We will segment twice the image in blocks:
- Firstly, we partition the image in destination or range blocks \(R_1, ..., R_L\). These blocks are disjoint and they cover the whole image.
- Then, we segment the image in source or domain blocks \(D_1, ..., D_K\). These blocks are not necessarily disjoint and neither they necessarily cover the image.
For instance, we can segment the image like this:
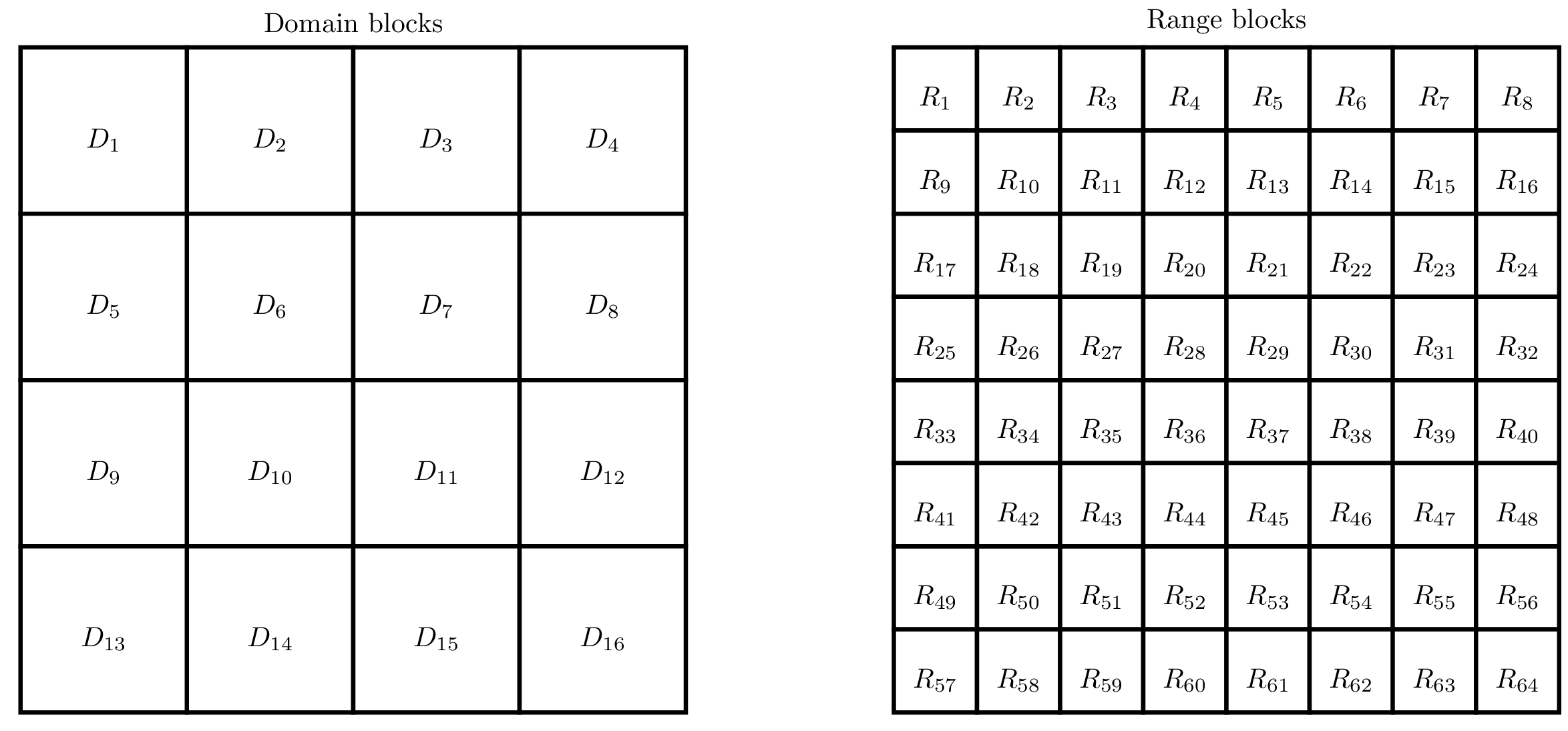
Then, for each range block \(R_l\), we will choose a domain block \(D_{k_l}\) and a mapping \(f_l : [0, 1]^{D_{k_l}} \rightarrow [0, 1]^{R_{l}}\).
Finally, we can define our function \(f\) as:
\[f(x)_{ij} = f_l(x_{D_{k_l}})_{ij} \text{ if } (i, j) \in R_l\]Claim: If all \(f_l\) are contractions then \(f\) is a contraction.
Let \(x, y \in E\) and suppose that all \(f_l\) are contractions with contractivity factor \(s_l\). Then we have that:
$$ \begin{alignat*}{2} d(f(x), f(y))^2 & = \sum_{i=1}^{h}{\sum_{j=1}^{w}{(f(x)_{ij}-f(y)_{ij})^2}} \text{ by definition of } d \\ & = \sum_{l=1}^L{\sum_{(i,j) \in R_l}{(f(x)_{ij}-f(y)_{ij})^2}} \text{ because } (R_l) \text{ is a partition} \\ & = \sum_{l=1}^L{\sum_{(i,j) \in R_l}{(f_l(x_{D_{k_l}})_{ij}-f_l(y_{D_{k_l}})_{ij})^2}} \text{ by definition of } f \\ & = \sum_{l=1}^L{d(f_l(x_{D_{k_l}}), f_l(y_{D_{k_l}}))^2} \text{ by definition of } d \\ & \leq \sum_{l=1}^L{s_l^2d(x_{D_{k_l}}, y_{D_{k_l}})^2} \text{ because the } (f_l) \text{ are contractions} \\ & \leq \underset{l}{\max}{s_l^2}\sum_{l=1}^L{d(x_{D_{k_l}}, y_{D_{k_l}})^2} \\ & = \underset{l}{\max}{s_l^2}\sum_{l=1}^L{\sum_{(i,j) \in R_l}{(x_{ij}-y_{ij})^2}} \text{ by definition of } d \\ & = \underset{l}{\max}{s_l^2}\sum_{i=1}^{h}{\sum_{j=1}^{w}{(x_{ij}-y_{ij})^2}} \text{ because } (R_l) \text{ is a partition} \\ & = \underset{l}{\max}{s_l^2}d(x, y)^2 \text{ by definition of } d \\ \end{alignat*} $$It remains one question to answer to: How to choose \(D_{k_l}\) and \(f_l\)?
The Collage Theorem suggests us a way to choose them: if \(x_{R_l}\) is near to \(f(x_{D_{k_l}})\) for all \(l\) then \(x\) is near to \(f(x)\) and according to the Collage Theorem \(x\) and \(x_0\) will be near too.
Thus, we will, independently for each \(l\), construct lots of contractions from each \(D_{k}\) to \(R_l\) and select the best one. We will show all the nitty-gritty details in the next section.
Implementation
In each section, I will copy the interesting snippets of code but you can find the whole script here.
Segmentations
I keep things really simple. The source blocks and the destination blocks segment the image as a grid, as on the image above.
The size of the blocks are powers of two as it makes things easier. The source blocks are 8 by 8 while the destination blocks are 4 by 4.
There exist more advanced schemes for segmentation. For instance, we can use a quadtree to segment more the areas with lots of details.
Transformations
In this section, we will show how to construct the contractions from \(D_{k}\) to \(R_l\).
Remember that we want to generate a mapping \(f_l\) such that \(f(x_{D_k})\) is near to \(x_{R_l}\). So, the more mappings we generate, the more likely we are to find a good one.
However, the quality of the compression depends on the number of bits necessary to save \(f_l\). So if we have a set of functions that is too large, the compression will be bad. There is a tradeoff to find.
I chose that \(f_l\) will have the following form: \(f_l(x_{D_k}) = s \times rotate_{\theta}(flip_d(reduce(x_{D_k}))) + b\)
where \(reduce\) is a function to go from 8 by 8 blocks to 4 by 4 blocks, \(flip\) and \(rotate\) are affine transformations, \(s\) changes the contrast and \(b\) the brightness.
The function reduce reduces the size of an image by averaging neighborhoods:
def reduce(img, factor):
result = np.zeros((img.shape[0] // factor, img.shape[1] // factor))
for i in range(result.shape[0]):
for j in range(result.shape[1]):
result[i,j] = np.mean(img[i*factor:(i+1)*factor,j*factor:(j+1)*factor])
return result
The function rotate simply rotates by the given angle the image:
def rotate(img, angle):
return ndimage.rotate(img, angle, reshape=False)
In order to preserve the shape of the image, the angle \(\theta\) will be in \(\{0^{\circ}, 90^{\circ}, 180^{\circ}, 270^{\circ}\}\).
The function flip flips the image if direction is equal to -1 and does not if it is equal to 1:
def flip(img, direction):
return img[::direction,:]
The whole transformation is done by the function apply_transformation:
def apply_transformation(img, direction, angle, contrast=1.0, brightness=0.0):
return contrast*rotate(flip(img, direction), angle) + brightness
We need 1 bit to remember if we flip or not and 2 bits for the angle of rotation. Moreover, if we save \(s\) and \(b\) using 8 bits each then we need only 19 bits in total to save the transformation.
Moreover, we should check that these functions are contractions. The proof is a bit tedious and we do not care much. Maybe I will add it in appendix later.
Compression
The algorithm for compression is simple. First we generate all possible affine transformations of all source blocks using the function generate_all_transformed_blocks:
def generate_all_transformed_blocks(img, source_size, destination_size, step):
factor = source_size // destination_size
transformed_blocks = []
for k in range((img.shape[0] - source_size) // step + 1):
for l in range((img.shape[1] - source_size) // step + 1):
# Extract the source block and reduce it to the shape of a destination block
S = reduce(img[k*step:k*step+source_size,l*step:l*step+source_size], factor)
# Generate all possible transformed blocks
for direction, angle in candidates:
transformed_blocks.append((k, l, direction, angle, apply_transform(S, direction, angle)))
return transformed_blocks
Then for each destination block, we try all the previously generated transformed source blocks. For each we optimize the contrast and the brightness using the method find_contrast_and_brightness2 and if the tested transformation is the best we have seen so far, we saved it:
def compress(img, source_size, destination_size, step):
transformations = []
transformed_blocks = generate_all_transformed_blocks(img, source_size, destination_size, step)
for i in range(img.shape[0] // destination_size):
transformations.append([])
for j in range(img.shape[1] // destination_size):
print(i, j)
transformations[i].append(None)
min_d = float('inf')
# Extract the destination block
D = img[i*destination_size:(i+1)*destination_size,j*destination_size:(j+1)*destination_size]
# Test all possible transformations and take the best one
for k, l, direction, angle, S in transformed_blocks:
contrast, brightness = find_contrast_and_brightness2(D, S)
S = contrast*S + brightness
d = np.sum(np.square(D - S))
if d < min_d:
min_d = d
transformations[i][j] = (k, l, direction, angle, contrast, brightness)
return transformations
To find the best contrast and brightness, the method find_contrast_and_brightness2 simply solves a least square problem:
def find_contrast_and_brightness2(D, S):
# Fit the contrast and the brightness
A = np.concatenate((np.ones((S.size, 1)), np.reshape(S, (S.size, 1))), axis=1)
b = np.reshape(D, (D.size,))
x, _, _, _ = np.linalg.lstsq(A, b)
return x[1], x[0]
Decompression
The decompression algorithm is even simpler. We just start from a completely random image and then we apply the contraction \(f\) several times:
def decompress(transformations, source_size, destination_size, step, nb_iter=8):
factor = source_size // destination_size
height = len(transformations) * destination_size
width = len(transformations[0]) * destination_size
iterations = [np.random.randint(0, 256, (height, width))]
cur_img = np.zeros((height, width))
for i_iter in range(nb_iter):
print(i_iter)
for i in range(len(transformations)):
for j in range(len(transformations[i])):
# Apply transform
k, l, flip, angle, contrast, brightness = transformations[i][j]
S = reduce(iterations[-1][k*step:k*step+source_size,l*step:l*step+source_size], factor)
D = apply_transformation(S, flip, angle, contrast, brightness)
cur_img[i*destination_size:(i+1)*destination_size,j*destination_size:(j+1)*destination_size] = D
iterations.append(cur_img)
cur_img = np.zeros((height, width))
return iterations
It works because the contraction has a unique fixed point and whatever initial image we choose, we will tend to it.
I think, it is time for a little example. We will try to compress and decompress this image of a monkey:
The function test_greyscale loads the image compresses it, decompresses and shows each iteration of the decompression:
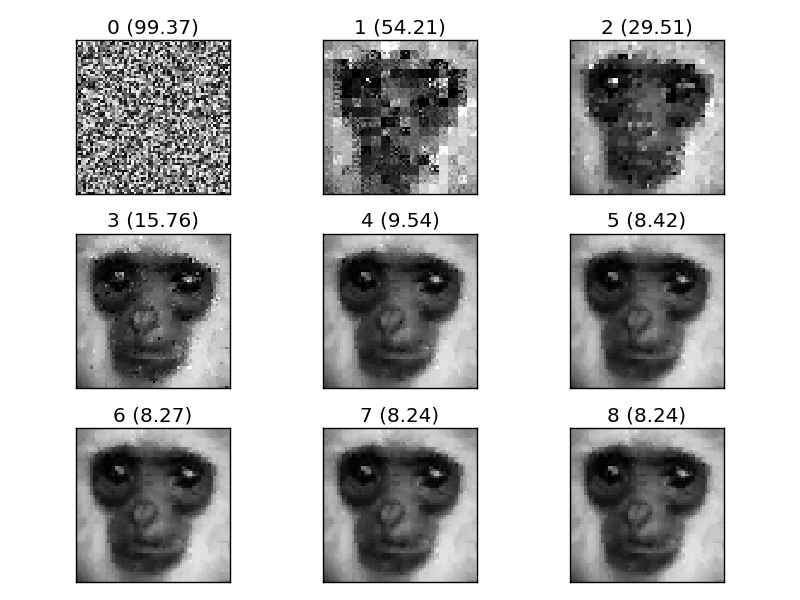
Not bad for this very simple implementation!
RGB Images
A very naive solution to compress RGB images is to compress the three channels separately:
def compress_rgb(img, source_size, destination_size, step):
img_r, img_g, img_b = extract_rgb(img)
return [compress(img_r, source_size, destination_size, step), \
compress(img_g, source_size, destination_size, step), \
compress(img_b, source_size, destination_size, step)]
And to decompress, we just decompress the three channels separately and then we assemble the three channels:
def decompress_rgb(transformations, source_size, destination_size, step, nb_iter=8):
img_r = decompress(transformations[0], source_size, destination_size, step, nb_iter)[-1]
img_g = decompress(transformations[1], source_size, destination_size, step, nb_iter)[-1]
img_b = decompress(transformations[2], source_size, destination_size, step, nb_iter)[-1]
return assemble_rbg(img_r, img_g, img_b)
Another very simple solution would be to use the same contraction for the three channels as they often are very similar.
If you would like to see it works, you can run the function test_rgb:
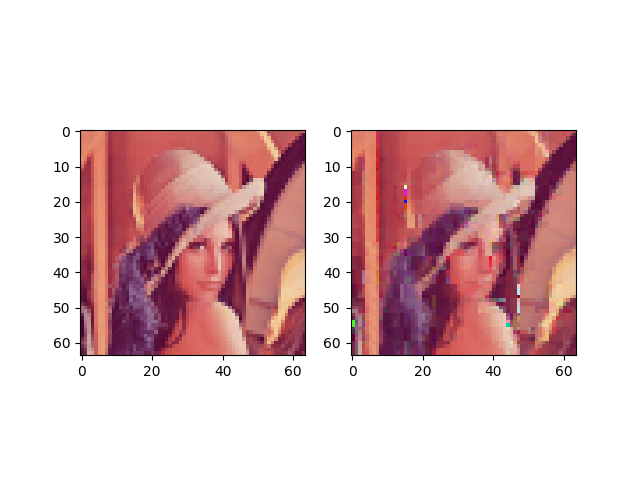
There are some artifacts. This method is maybe too naive to give good results.
To Go Further
If you would like to learn more about fractal image compression, I can suggest you to read Fractal and Wavelet Image Compression Techniques by Stephen Welstead. It is easy to read and explains more advanced techniques.
If you have any suggestion or question, do not hesitate to leave a comment below.
If you are interested in my adventures during the development of Vagabond, you can follow me on Twitter.
