pvigier's blog
computer science, programming and other ideas
Perlin Noise With Numpy
Hi everyone, I have written an implementation of Perlin noise with numpy that is pretty fast, and I want to share it with you. The code is available here.
Perlin Noise
My code looks like the original implementation. The only difference is that I tried to use the vectorized operations of numpy as much as possible instead of for loops. Because as you may know, loops are really slow in Python.
Here is the code:
def generate_perlin_noise_2d(shape, res):
def f(t):
return 6*t**5 - 15*t**4 + 10*t**3
delta = (res[0] / shape[0], res[1] / shape[1])
d = (shape[0] // res[0], shape[1] // res[1])
grid = np.mgrid[0:res[0]:delta[0],0:res[1]:delta[1]].transpose(1, 2, 0) % 1
# Gradients
angles = 2*np.pi*np.random.rand(res[0]+1, res[1]+1)
gradients = np.dstack((np.cos(angles), np.sin(angles)))
g00 = gradients[0:-1,0:-1].repeat(d[0], 0).repeat(d[1], 1)
g10 = gradients[1:,0:-1].repeat(d[0], 0).repeat(d[1], 1)
g01 = gradients[0:-1,1:].repeat(d[0], 0).repeat(d[1], 1)
g11 = gradients[1:,1:].repeat(d[0], 0).repeat(d[1], 1)
# Ramps
n00 = np.sum(grid * g00, 2)
n10 = np.sum(np.dstack((grid[:,:,0]-1, grid[:,:,1])) * g10, 2)
n01 = np.sum(np.dstack((grid[:,:,0], grid[:,:,1]-1)) * g01, 2)
n11 = np.sum(np.dstack((grid[:,:,0]-1, grid[:,:,1]-1)) * g11, 2)
# Interpolation
t = f(grid)
n0 = n00*(1-t[:,:,0]) + t[:,:,0]*n10
n1 = n01*(1-t[:,:,0]) + t[:,:,0]*n11
return np.sqrt(2)*((1-t[:,:,1])*n0 + t[:,:,1]*n1)
If you are familiar with Perlin noise, nothing should surprise you. Otherwise, I can suggest you to read the first pages of this article which explains Perlin noise very well in my opinion.
An example of what the function generates:
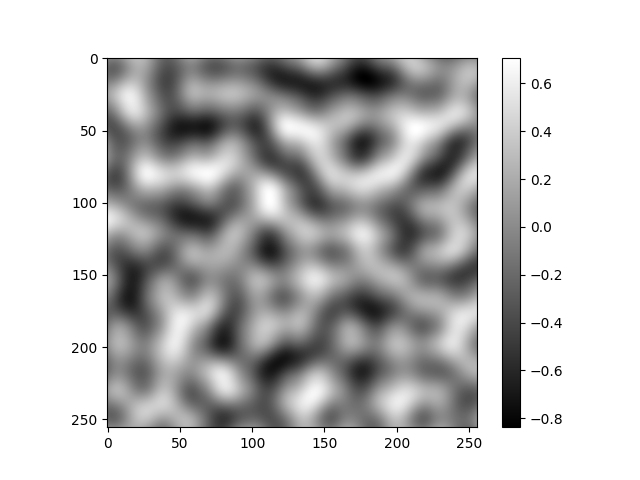
I normalized the gradients so that the noise is always between -1 and 1.
Fractal Noise
Using the previous function, I wrote another that combines several octaves of Perlin noise to generate fractal noise:
def generate_fractal_noise_2d(shape, res, octaves=1, persistence=0.5):
noise = np.zeros(shape)
frequency = 1
amplitude = 1
for _ in range(octaves):
noise += amplitude * generate_perlin_noise_2d(shape, (frequency*res[0], frequency*res[1]))
frequency *= 2
amplitude *= persistence
return noise
An example of what we can obtain:
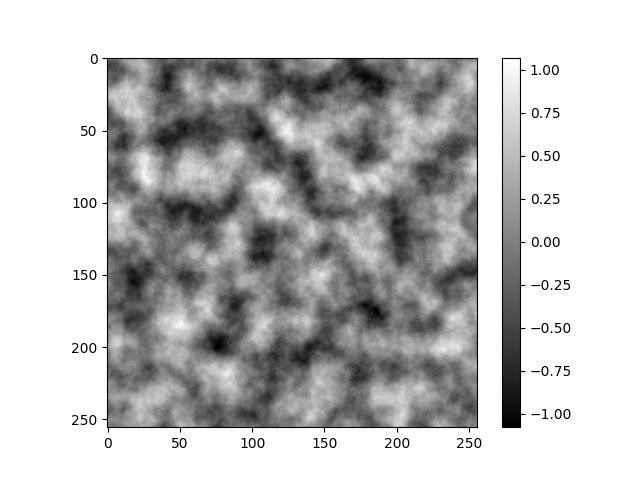
The fractal noise is not always between -1 and 1 but between -2 and 2 if you keep the persistence equals to 0.5.
I will show you in future articles how I used Perlin noise and fractal noise in my projects.
If you are interested in my adventures during the development of Vagabond, you can follow me on Twitter.
