pvigier's blog
computer science, programming and other ideas
Vagabond – Dungeon and Cave Generation – Part 1

I am sorry, there was no article last week as I was on vacation.
But, this week I started working on a new topic: dungeon and cave generation. I used space partitioning to generate rooms, maze generation algorithms to generate the corridors and cellular automata to have a more organic look and feel for caves. Let’s dive in the details!
Space Partitioning
There are many ways (random placement, agent based, using separation steering behavior or a physics engine, etc.) to create rooms for a dungeon. But my favorite method is space partitioning because it is controllable and easily expandable.
There are also many ways to split the space: grid partitioning, binary space partitioning, quad tree space partitioning, Voronoi diagrams, etc. I chose to use binary space partitioning this time as it is well suited to generate rectangular rooms. This method was popularized by an article on RogueBasin.
The only difficulty with this algorithm is to choose the split position. Indeed, if we do not set any constraint on the split position, we obtain weird space partitions:

There are several ways to avoid this behavior. One is to constrain the split to be between two ratios of the side length for instance between 30% and 70% or 40% and 60%. Another method is to use a normal or a binomial distribution instead of a uniform distribution, it is then more likely to split near the center of the side than its extremities. These methods fix the issue but it is hard to understand exactly how the parameters modify the final result.
So I use another method that has the advantage of having only one parameter which is easily understandable: the maximum allowed ratio between the length and the width of cells. When I sample a new split, I firstly compute the minimum value and the maximum value it can take so that the two new cells have their ratio below the limit then I sample uniformly between the two bounds. Here is the result when I vary the maximum allowed ratio:

A maximum ratio between 2.0 and 3.0 gives good results:

Room Generation
The next step is to generate a room inside each cell. There is no special issue here, I just set some constraints so that the rooms are not too small nor too close to the walls of the cells.
Here are the results:

Edge Selection
Commonly in dungeon generators based on binary space partitioning, the binary tree used during space partitioning is used again for corridor generation. I did not do that because, in my opinion, it is quite limited.
Instead, during space partitioning, I maintain a half-edge data structure which allows to know which cells are next to each other. Thus, I have graphs like that:
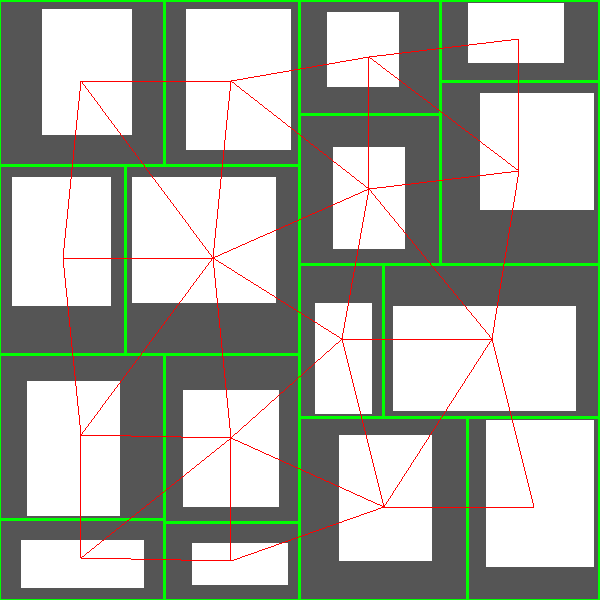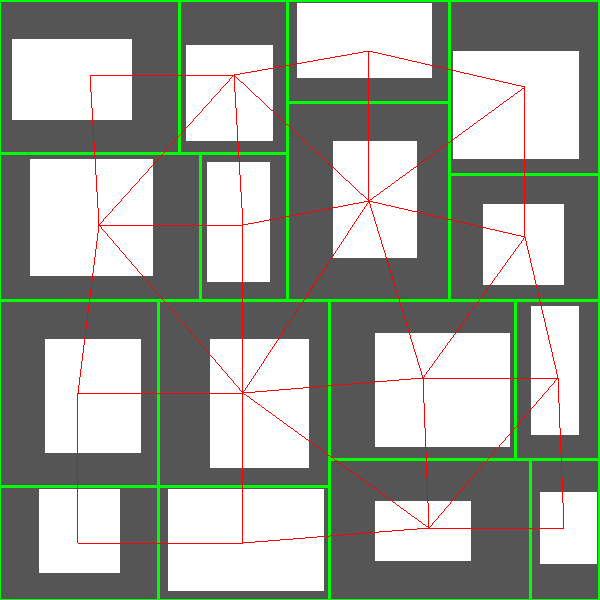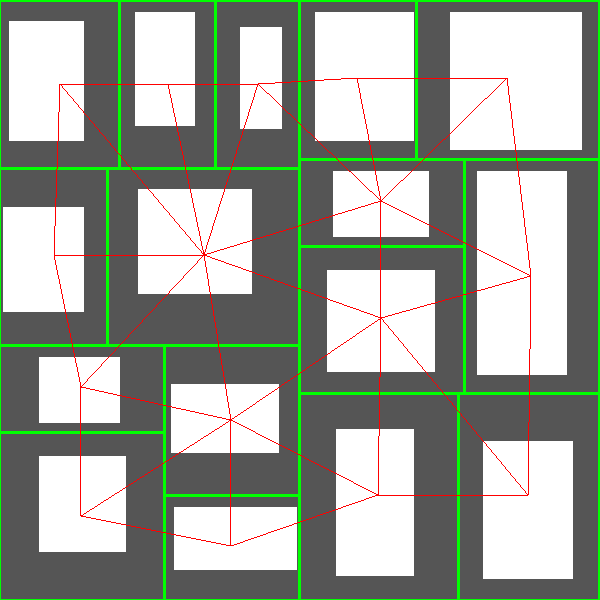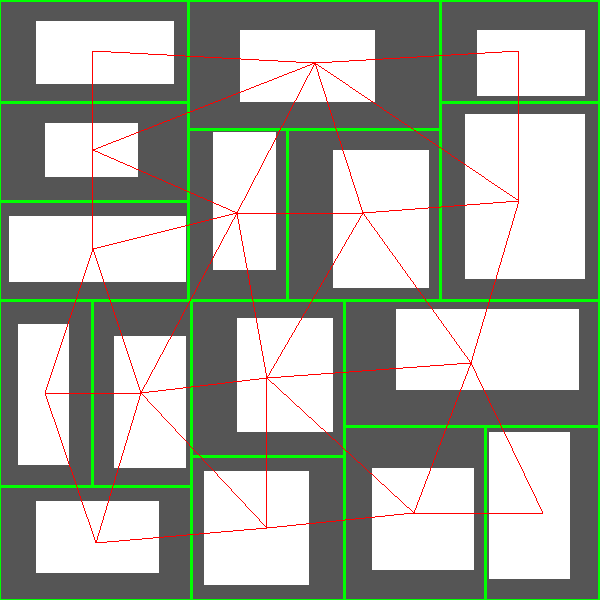
There are three advantages with this approach. The first one is that if later I want to change the method used for space partitioning, the rest of the generator is still valid as it only takes a half-edge data structure as input. The second one is that I can now use any maze generation algorithm to select the edges that will become corridors. The third one is that if I want to add cycles in the dungeon, I can easily do so.
For now, I simply use Kruskal algorithm with Manhattan distance to select the edges. Here are the results:
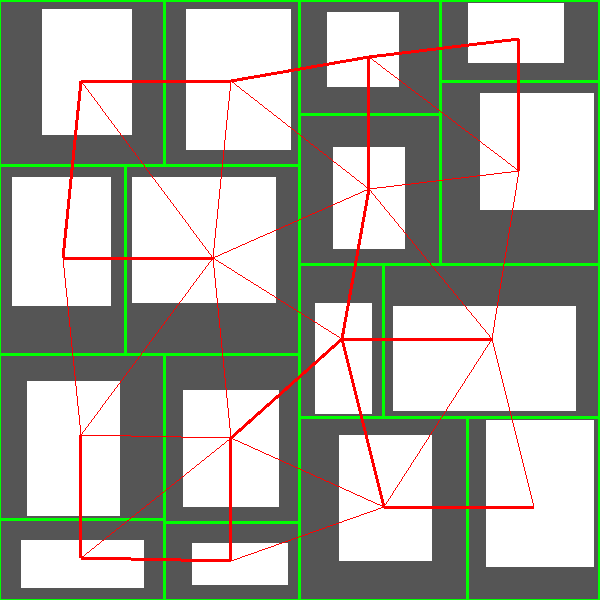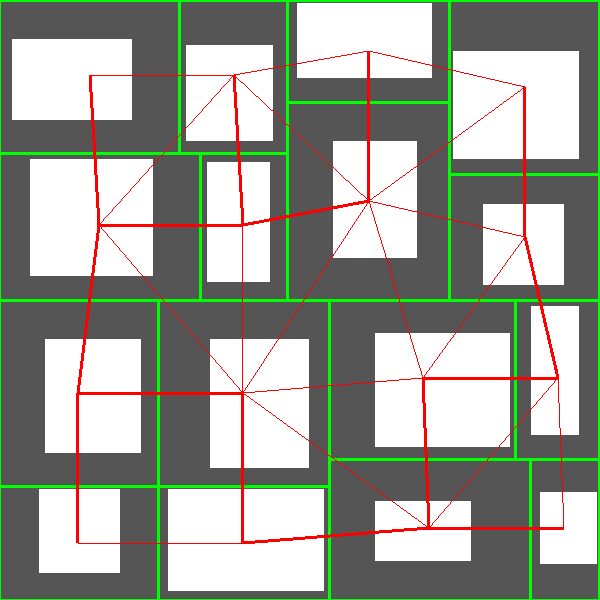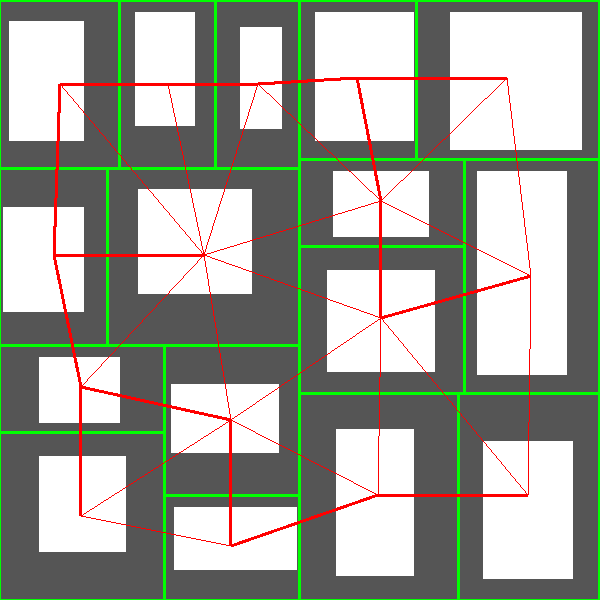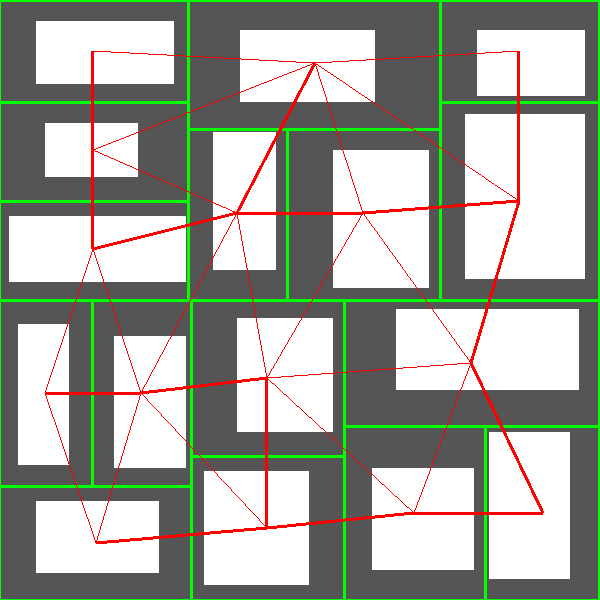
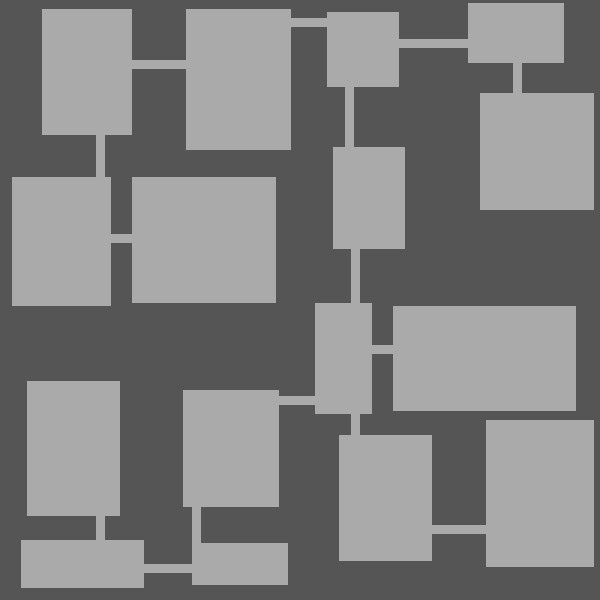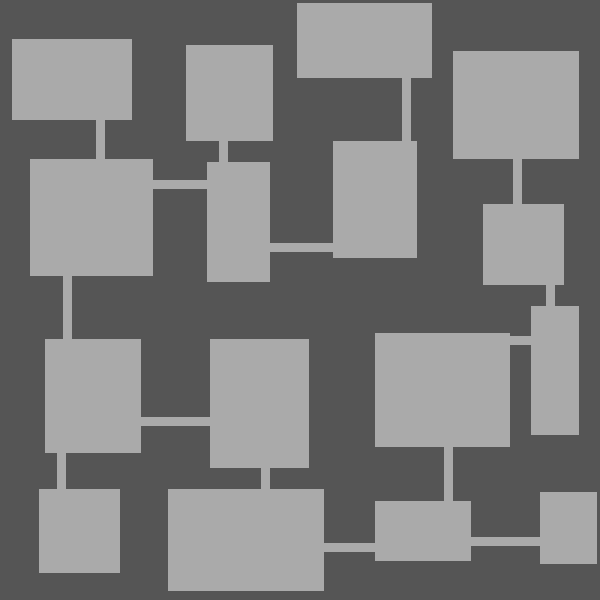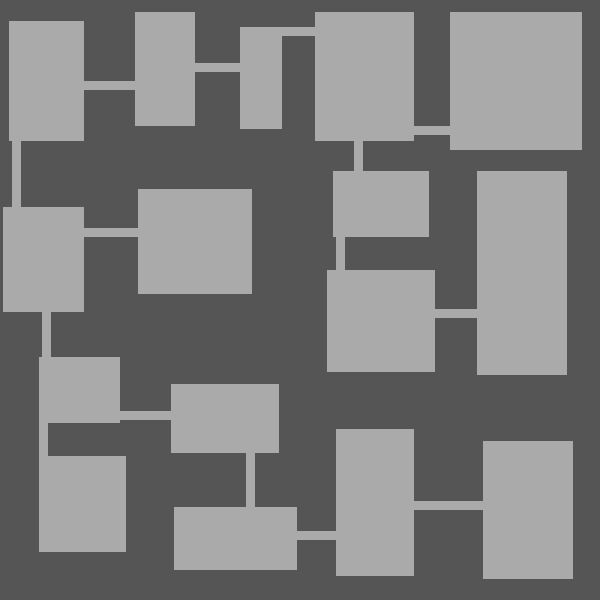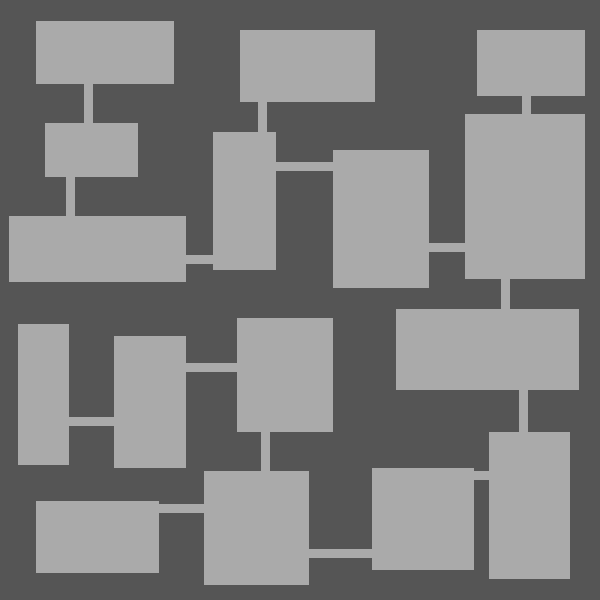
Corridor Generation
The next step is the generation of corridors from the selected edges. This is maybe the trickiest part of the generator as we need to be careful that no corridor crosses another one.
Here are the results:
Cave Generation
The previous results are fine for dungeons, crypts or other man-made structures but I would like a more organic aspect for caves or mines. The classic method to generate caves is to use a cellular automaton as described in this article on RogueBasin. The big issue with cellular automata is that the results are not really controllable.
My idea is to still use cellular automata to obtain an organic look but I set constraints to have a controllable result. Instead of using only two states: dead or alive, I use four: definitively dead, dead, alive, definitively alive. The “definitively” states cannot change from one step to another, they serve to constrain the result.
The rooms and the corridors we have generated in the previous steps are filled with definitively alive cells. Thus, we are still have a notion rooms and we are sure that they are connected to each other. The edges that were not selected are filled with definitively dead cells to make sure that no new path from one room to another appears. Finally around the rooms and the corridors we randomly set some cells to alive. Here is the initial configuration:

Then we run the cellular automaton to obtain the desired organic look:

Here are some more results:

One thing that I will surely implement later is a flood fill to remove unreachable parts.
Conclusion
This is the first leg of the long journey of building an interesting dungeon generator. I am happy with the results so far. I am especially proud of the constrained cellular automaton method to have controllable and organic caves. I also like the fact that each step of the generation is separated from the others and can be modified independently.
The next step is to generate tiles from the output of this generator to have much more appealing dungeons.
See you next week for more!
If you are interested in my adventures during the development of Vagabond, you can follow me on Twitter.
