pvigier's blog
computer science, programming and other ideas
3D Perlin Noise With Numpy
Few weeks ago, a professor from the university of Waterloo contacted me to ask if it was possible to adapt my code for 2D Perlin noise to 3D Perlin noise.
I was very happy that someone was interested by this piece of code. After some thoughts, I answer him that it was possible and I decided to do it.
I move the old code which generates 2D Perlin noise in the file perlin2d.py and I place the code described below for 3D Perlin noise in the file perlin3d.py. You can find all the code in this github repo.
Code
The only difficulty to generalize the 2D code to 3D is the increased number of cases in each step. Besides, we need to be careful with indices:
def generate_perlin_noise_3d(shape, res):
def f(t):
return 6*t**5 - 15*t**4 + 10*t**3
delta = (res[0] / shape[0], res[1] / shape[1], res[2] / shape[2])
d = (shape[0] // res[0], shape[1] // res[1], shape[2] // res[2])
grid = np.mgrid[0:res[0]:delta[0],0:res[1]:delta[1],0:res[2]:delta[2]]
grid = grid.transpose(1, 2, 3, 0) % 1
# Gradients
theta = 2*np.pi*np.random.rand(res[0]+1, res[1]+1, res[2]+1)
phi = 2*np.pi*np.random.rand(res[0]+1, res[1]+1, res[2]+1)
gradients = np.stack((np.sin(phi)*np.cos(theta), np.sin(phi)*np.sin(theta), np.cos(phi)), axis=3)
gradients[-1] = gradients[0]
g000 = gradients[0:-1,0:-1,0:-1].repeat(d[0], 0).repeat(d[1], 1).repeat(d[2], 2)
g100 = gradients[1: ,0:-1,0:-1].repeat(d[0], 0).repeat(d[1], 1).repeat(d[2], 2)
g010 = gradients[0:-1,1: ,0:-1].repeat(d[0], 0).repeat(d[1], 1).repeat(d[2], 2)
g110 = gradients[1: ,1: ,0:-1].repeat(d[0], 0).repeat(d[1], 1).repeat(d[2], 2)
g001 = gradients[0:-1,0:-1,1: ].repeat(d[0], 0).repeat(d[1], 1).repeat(d[2], 2)
g101 = gradients[1: ,0:-1,1: ].repeat(d[0], 0).repeat(d[1], 1).repeat(d[2], 2)
g011 = gradients[0:-1,1: ,1: ].repeat(d[0], 0).repeat(d[1], 1).repeat(d[2], 2)
g111 = gradients[1: ,1: ,1: ].repeat(d[0], 0).repeat(d[1], 1).repeat(d[2], 2)
# Ramps
n000 = np.sum(np.stack((grid[:,:,:,0] , grid[:,:,:,1] , grid[:,:,:,2] ), axis=3) * g000, 3)
n100 = np.sum(np.stack((grid[:,:,:,0]-1, grid[:,:,:,1] , grid[:,:,:,2] ), axis=3) * g100, 3)
n010 = np.sum(np.stack((grid[:,:,:,0] , grid[:,:,:,1]-1, grid[:,:,:,2] ), axis=3) * g010, 3)
n110 = np.sum(np.stack((grid[:,:,:,0]-1, grid[:,:,:,1]-1, grid[:,:,:,2] ), axis=3) * g110, 3)
n001 = np.sum(np.stack((grid[:,:,:,0] , grid[:,:,:,1] , grid[:,:,:,2]-1), axis=3) * g001, 3)
n101 = np.sum(np.stack((grid[:,:,:,0]-1, grid[:,:,:,1] , grid[:,:,:,2]-1), axis=3) * g101, 3)
n011 = np.sum(np.stack((grid[:,:,:,0] , grid[:,:,:,1]-1, grid[:,:,:,2]-1), axis=3) * g011, 3)
n111 = np.sum(np.stack((grid[:,:,:,0]-1, grid[:,:,:,1]-1, grid[:,:,:,2]-1), axis=3) * g111, 3)
# Interpolation
t = f(grid)
n00 = n000*(1-t[:,:,:,0]) + t[:,:,:,0]*n100
n10 = n010*(1-t[:,:,:,0]) + t[:,:,:,0]*n110
n01 = n001*(1-t[:,:,:,0]) + t[:,:,:,0]*n101
n11 = n011*(1-t[:,:,:,0]) + t[:,:,:,0]*n111
n0 = (1-t[:,:,:,1])*n00 + t[:,:,:,1]*n10
n1 = (1-t[:,:,:,1])*n01 + t[:,:,:,1]*n11
return ((1-t[:,:,:,2])*n0 + t[:,:,:,2]*n1)
The adaptation of the code to generate 3D fractal is more direct and simpler:
def generate_fractal_noise_3d(shape, res, octaves=1, persistence=0.5):
noise = np.zeros(shape)
frequency = 1
amplitude = 1
for _ in range(octaves):
noise += amplitude * generate_perlin_noise_3d(shape, (frequency*res[0], frequency*res[1], frequency*res[2]))
frequency *= 2
amplitude *= persistence
return noise
Some Images
To finish this article, I put some gifs to visualize the generated 3D noise. I tweak a bit the code so that the noise is tileable along the x-axis, it makes the gif much more pleasant to watch.
Here is some 3D Perlin noise:
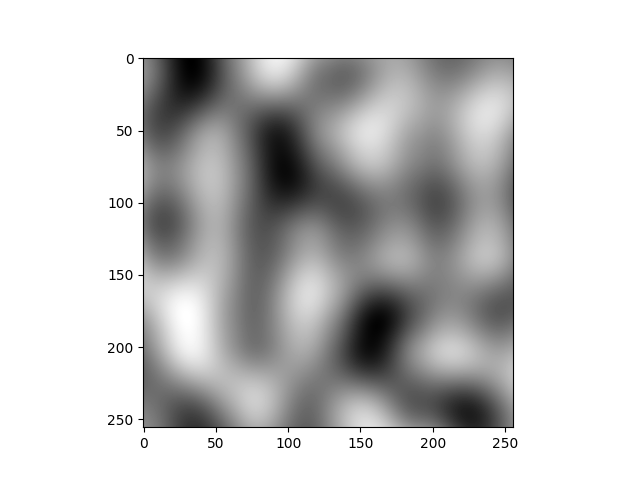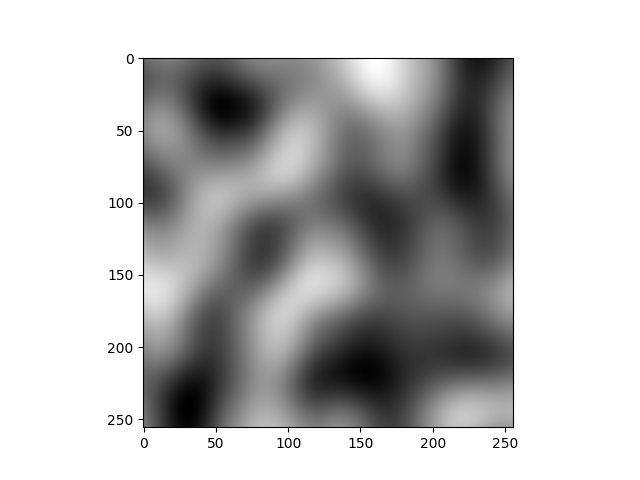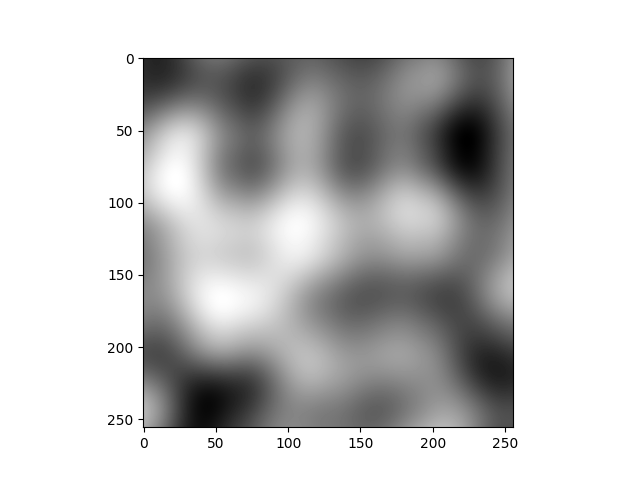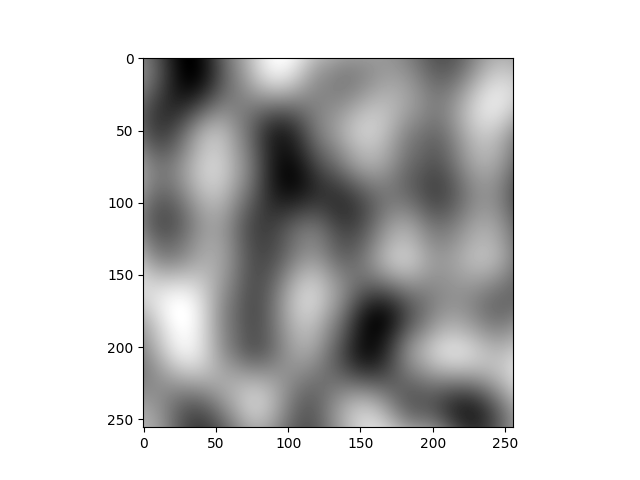
And here some 3D fractal noise:
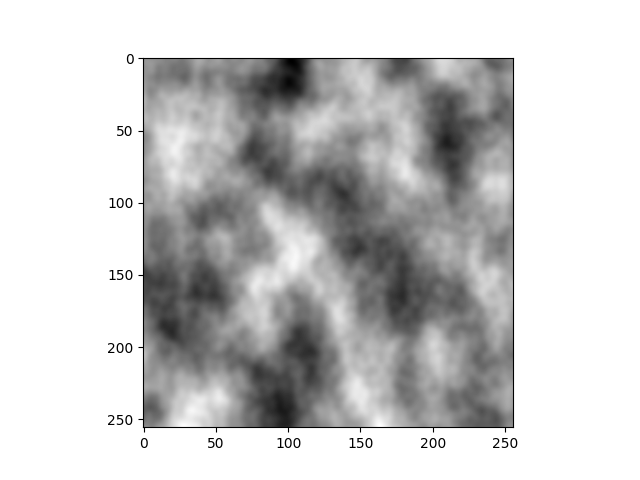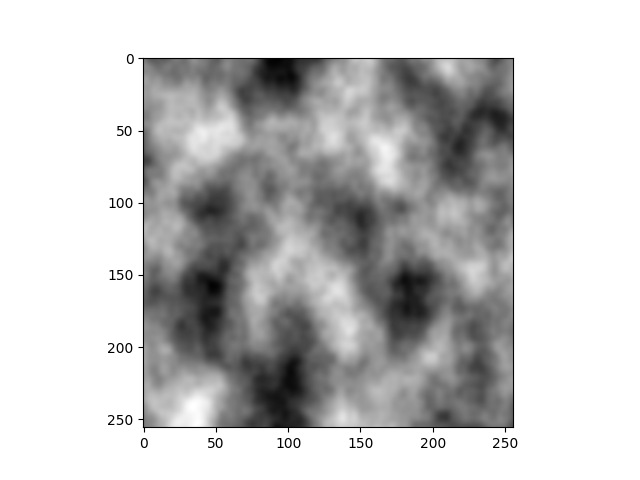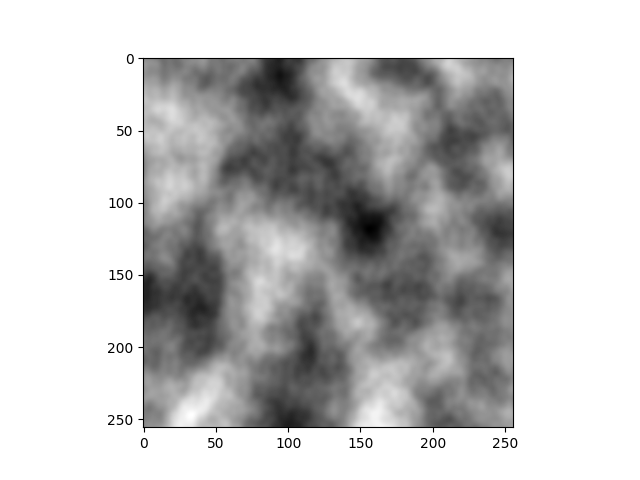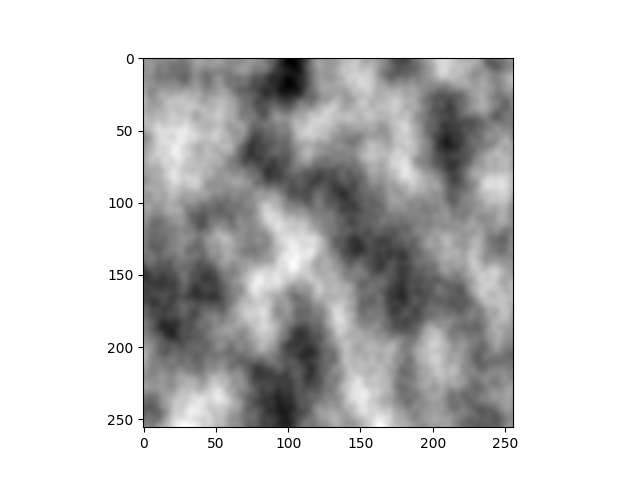
See you!
If you are interested in my adventures during the development of Vagabond, you can follow me on Twitter.
