Vagabond – Borders, Rivers, Cities and Roads

19 May 2019 by pierre

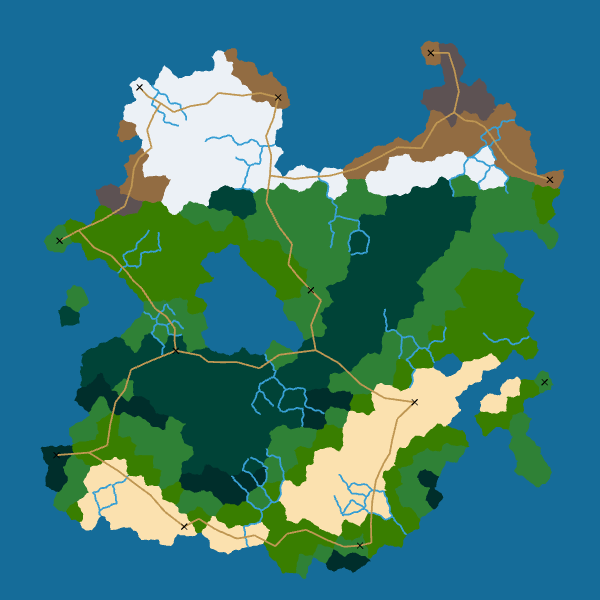
In this week’s devlog, I take up the map generator where I left it last week. I explain how I improved cell borders and added rivers, cities and roads to the map generator.

Borders

The first thing I did was working on improving the cell borders. I wanted something more natural than straight lines to separate the biomes.

I just use 1D Perlin noise to disturb the lines: each point of the line is displaced according to the value of noise.

There are mainly two parameters with which we can play: the frequency of the noise and the strength of the displacement. I made two gifs to show you what happens when we vary these parameters.

The frequency:

The strength:

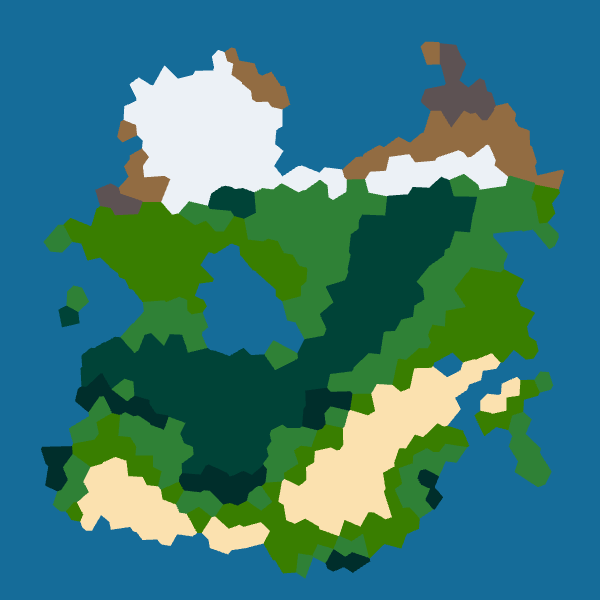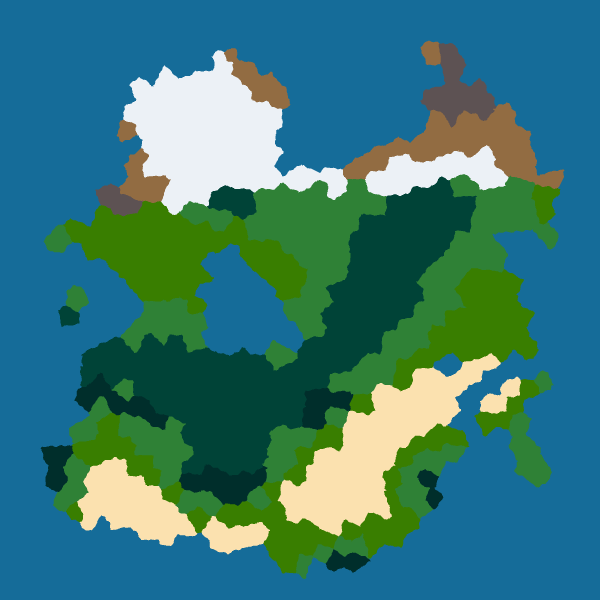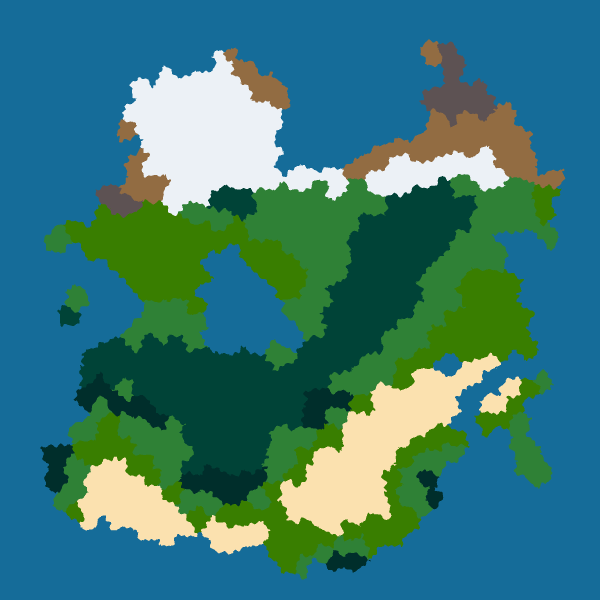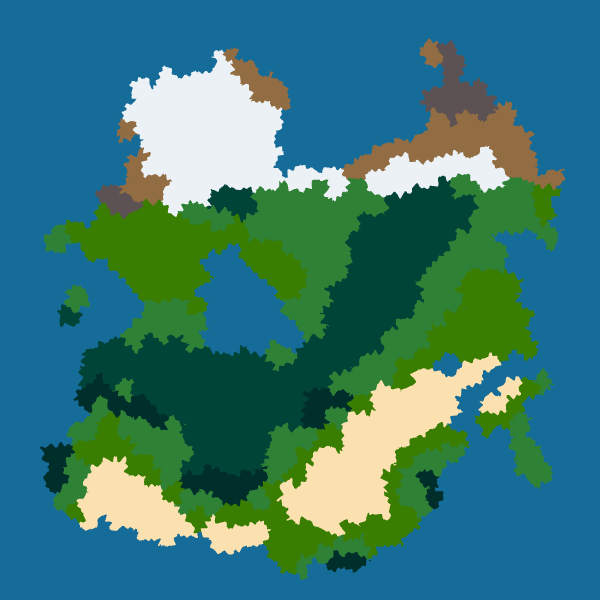
One idea may be to have different parameters for different biomes. For instance, we could increase the frequency for borders between snow and sea to have some fjords.

However, I want to keep things simple for now so I use a low frequency and low strength for all borders. Here are the results for four seeds:

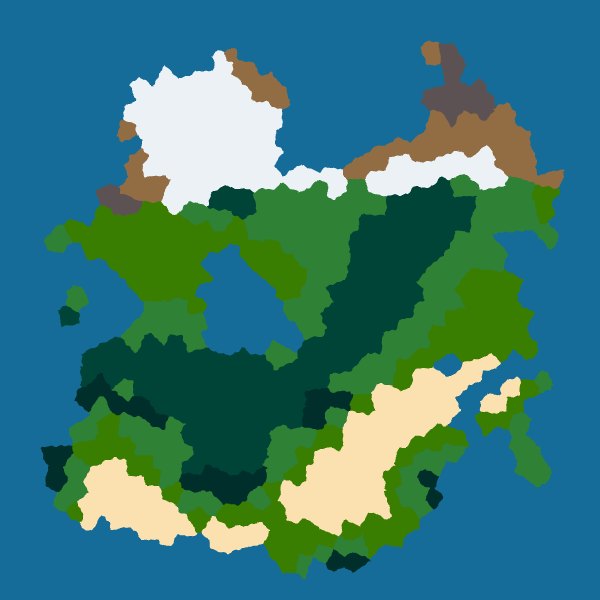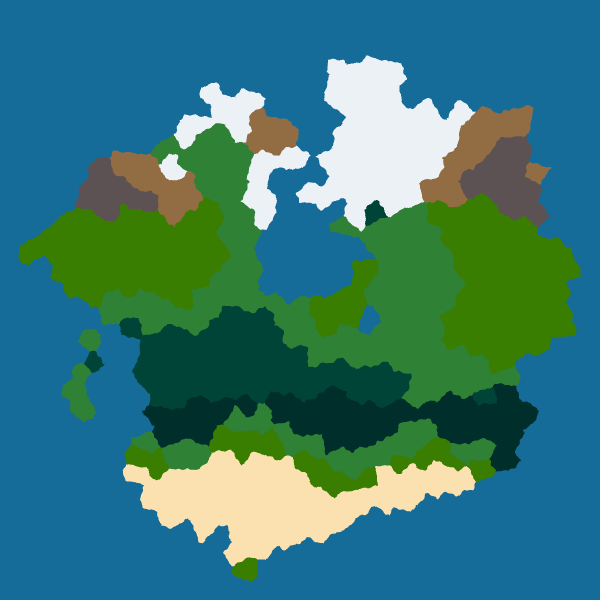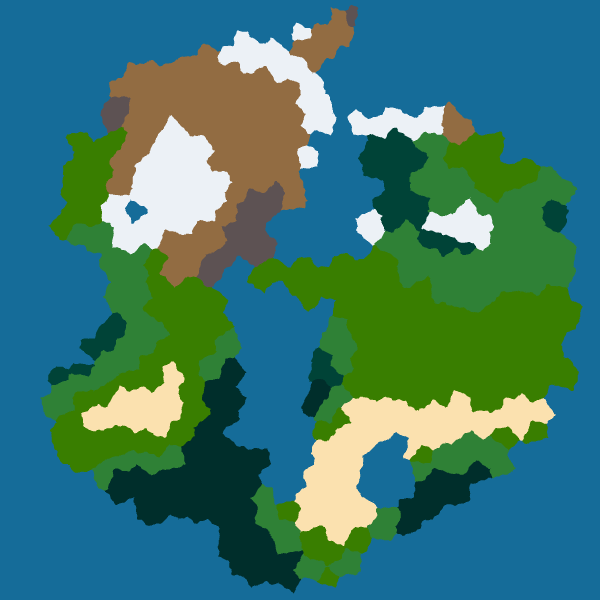Regions

One small thing I wanted to do last week was to unite adjacent cells with the same biome into a larger structure called a region. To achieve that, I just use a simple flood fill. Here are the results:

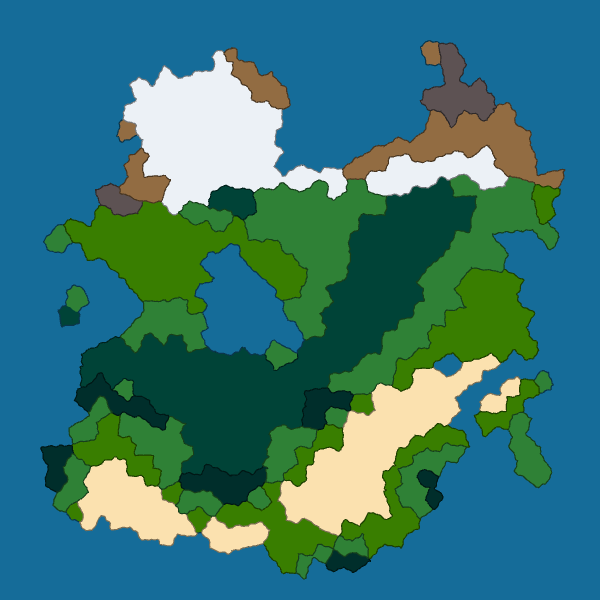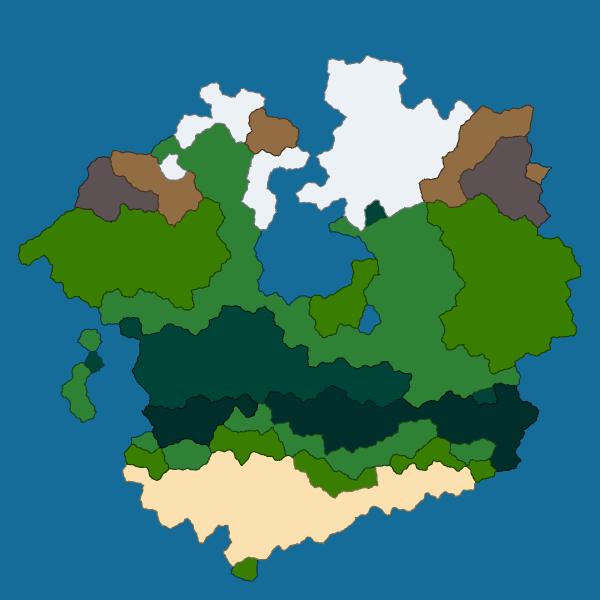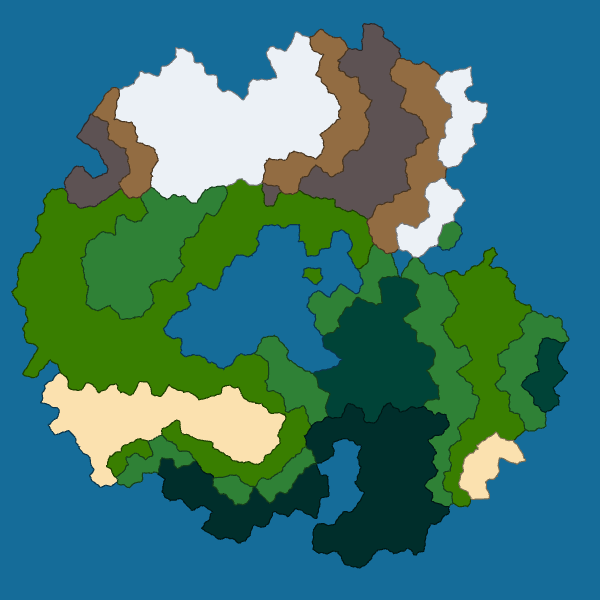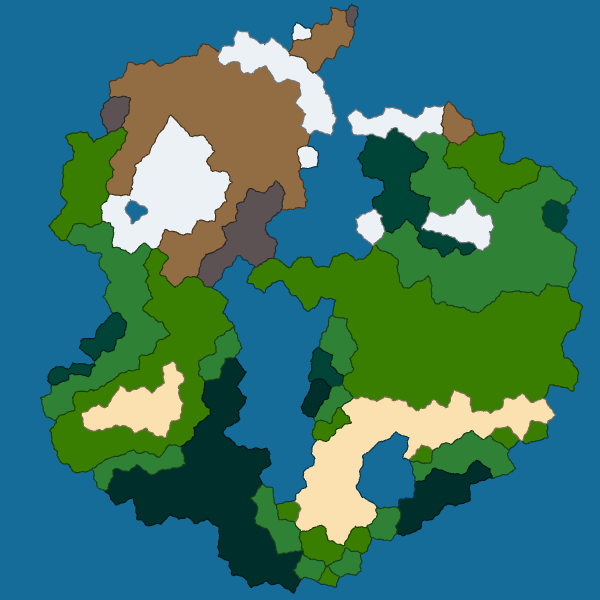I don’t know exactly what I will do with these regions yet. But it seems so natural to join adjacent cells that I had to do that. Maybe I will give them names so that NPC can refer to them.

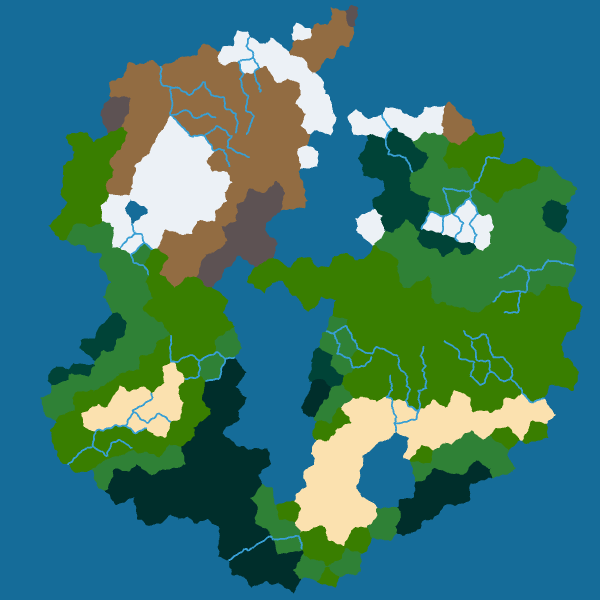
Rivers

Next, I worked on rivers. I decided that the rivers will be on the edges of cells. The reason is that only the edges can be in contact with seas, not the sites of Voronoi cells. Another reason is that rivers are good natural frontiers between biomes.

So the first thing to do is to compute the height of each vertex. I simply did an average of the height of adjacent cells. Then, I computed a downstream neighbor for each vertex, it is the lowest neighbor of this vertex that is also lower than this vertex. It may not be possible to find one for each vertex as a vertex could be a local minimum.

From that, we obtain a water flux:

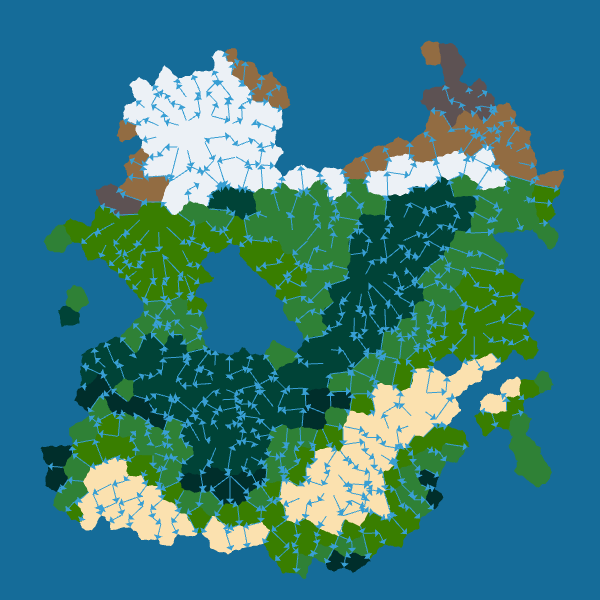
Then, I use a disjoint-set data structure to quickly find all the separated water networks.

Next, I reject all the networks that do not reach seas. It remains a list of candidate rivers from which I will select the actual rivers.

I have two criteria for the selection: I want the rivers to be well-spread over the map and to be interesting.

So, I compute a score for each river and I pick the one with the highest score. And I repeat the process until I reach the desired number of rivers.

The score is in two parts to take into account the two criteria. The first part assesses the proximity of the barycenter of the candidate river from the ones of already selected rivers.

In the animation below, you can observe how this part changes when there are more rivers (black is 0 and white is 1):

The second part is just the size (number of edges) of the river. And I just multiply the two parts to obtain the final score. This is pretty simple but it works well.

Moreover, we can also distort the river as we distorted the borders to obtain more natural rivers with meanders:

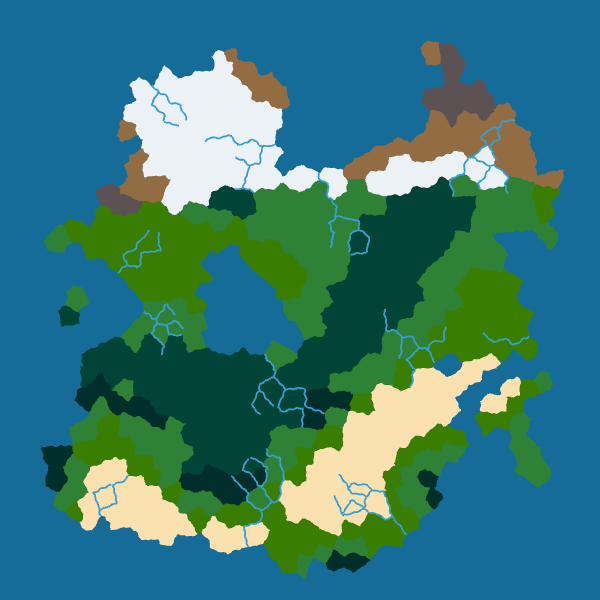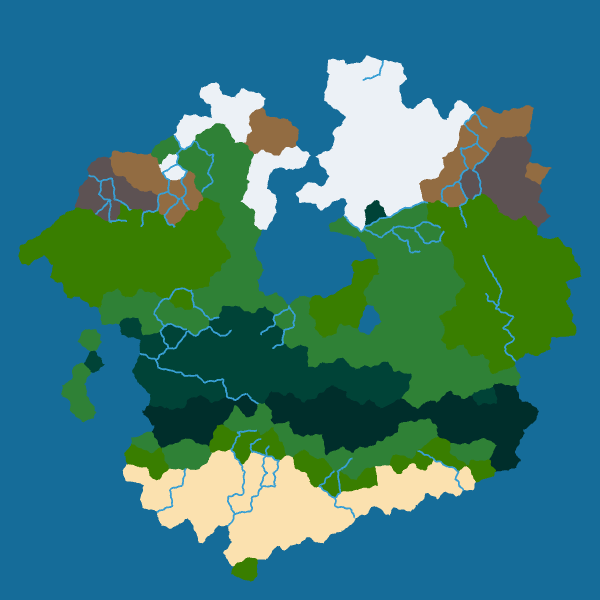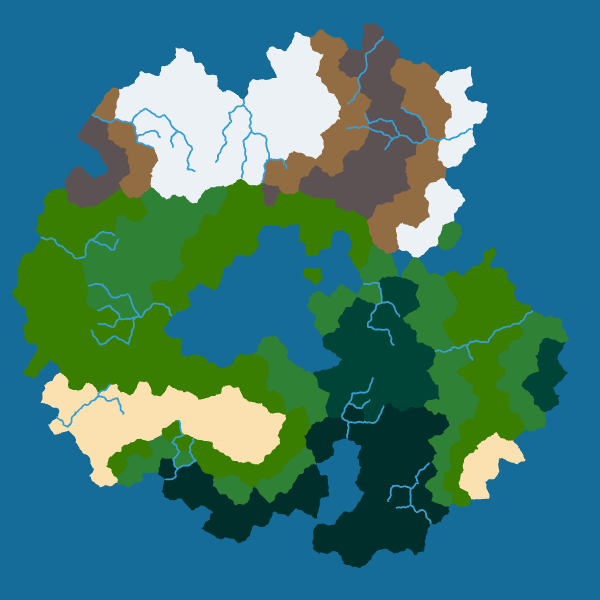Cities

The cities will be at the center of Voronoi cells. I use the same technique as before to choose the cells. I will give a score to each cell, put a city in the cell with the highest score and iterate until I have enough cities.

I firstly thought taking into account the rivers and shores to encourage the emergence of cities near sources of water. But the problem is that all the cities would be near rivers or seas and I would have no cities far inland.

So, I just use a simple score that only takes into account the proximity of a cell with already selected cities. And the results were sufficiently satisfying so I stopped there. You can see the results at the end of the next section.

Roads

Now that we have cities, we need some roads to connect them.

The idea is pretty simple, we will compute the shortest path between each pair of cities and add roads to link them. To compute the shortest paths, I use A* algorithm.

The problem is that in doing that, we will obtain a very dense network with a large amount of redundancy. To avoid that, when I compute the path between a new pair of cities I give a discount if it uses a road that already exists. For instance, creating a new road segment costs \(d\) where \(d\) is its distance while using an existing road segment costs only \(\gamma \times d\) where \(\gamma\) is the discount factor ranging between 0 and 1. Here is an animation that shows how the road network changes depending on the value of the discount factor:

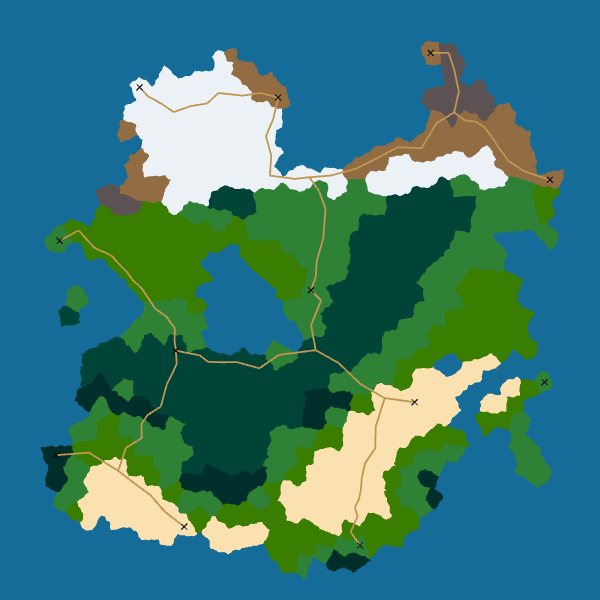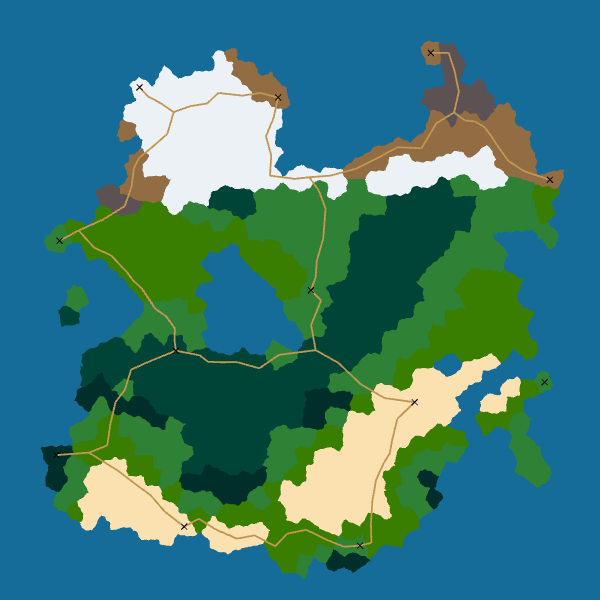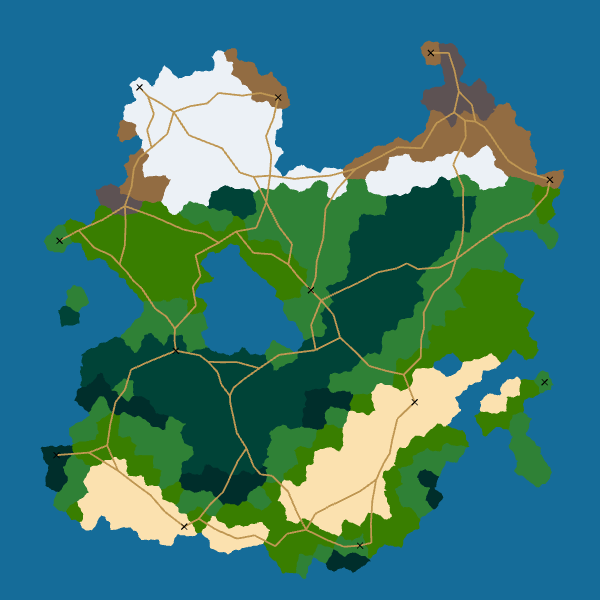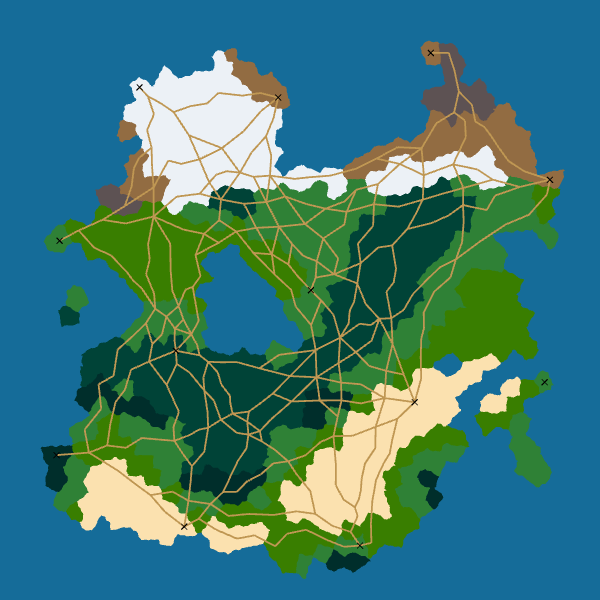
When \(\gamma\) is low, it is really advantageous to reuse an already built road segment so the road network is sparse. On the contrary, when \(\gamma\) is high, there is no big difference between reusing a road segment or constructing a new one so the network is dense.

Another issue is the order in which we process the pair of cities. Indeed, if we first compute the shortest paths between a city and all the others, we will have a network centered on this city like a star network:

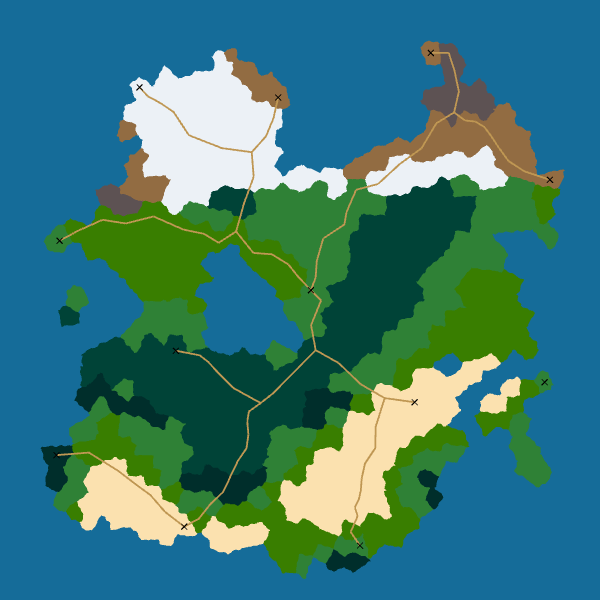
My idea to fix this issue is to first link near cities. Besides, I think it makes sense for a city to be connected first with its nearest neighbors and later with far cities. So I sort the pairs of cities by distance between the cities in the pair before processing them.

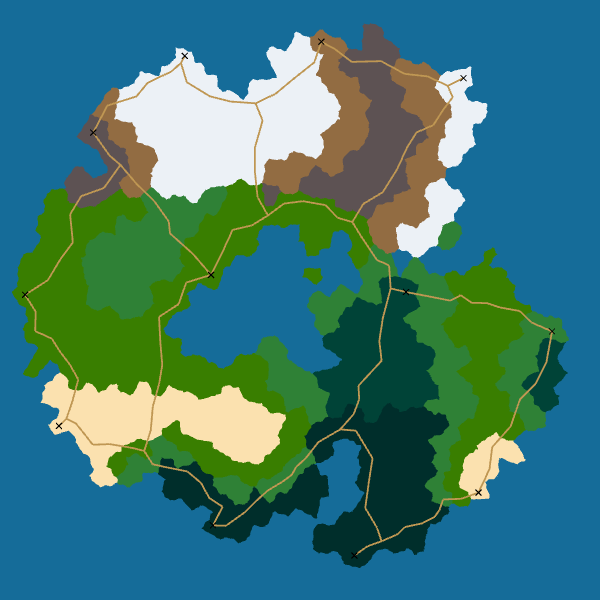
Here are the final results for roads:

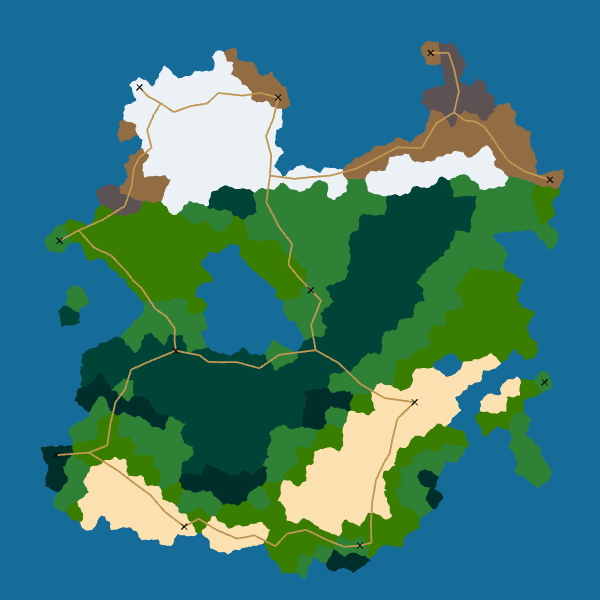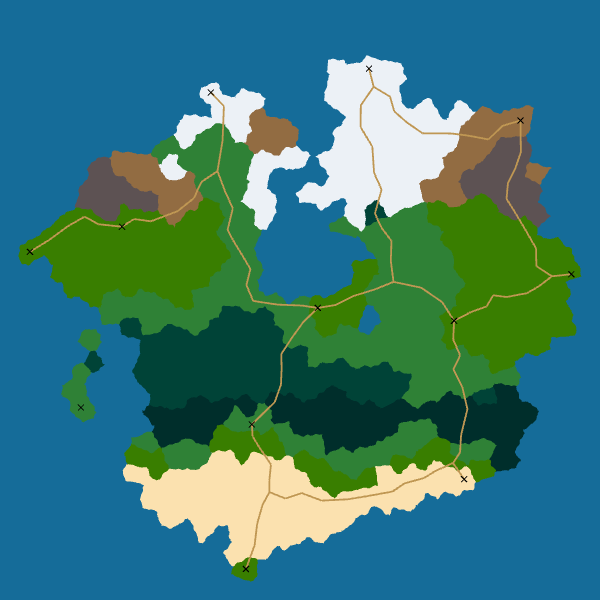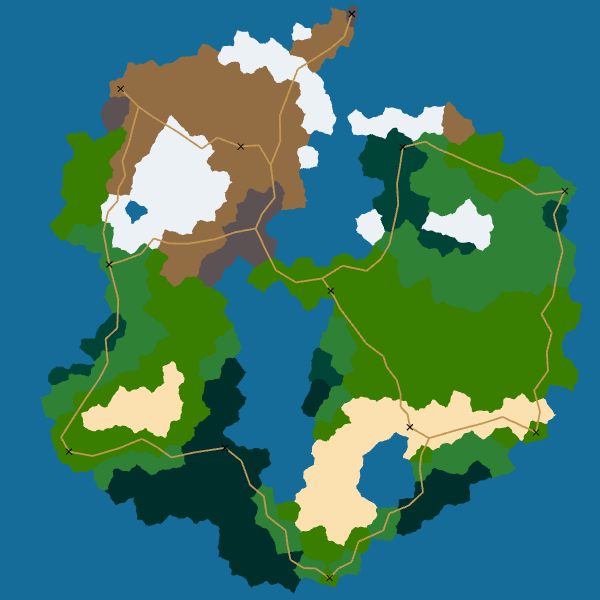I really like how the roads look. Moreover, the algorithm is robust: it always give a good result. And it is easily extensible: we can take into account elevation or biomes by modifying the cost function used by A*.

Conclusion

I try to keep things as simple as possible in order to have a solid base on which I can iterate.

Moreover, the generator is really fast: it takes less than 20ms to generate one of the map on my (cheap) laptop. Thus, I have some freedom to add complexity later.

The next step is to transform this symbolic map into a world where players would be able to move and interact. See you next week for more!

If you are interested in my adventures during the development of Vagabond, you can follow me on Twitter.

Tags: vagabond pcg