pvigier's blog
computer science, programming and other ideas
Perlin Noise With Numpy
Hi everyone, I have written an implementation of Perlin noise with numpy that is pretty fast, and I want to share it with you. The code is available here.
Perlin Noise
My code looks like the original implementation. The only difference is that I tried to use the vectorized operations of numpy as much as possible instead of for loops. Because as you may know, loops are really slow in Python.
Here is the code:
def generate_perlin_noise_2d(shape, res):
def f(t):
return 6*t**5 - 15*t**4 + 10*t**3
delta = (res[0] / shape[0], res[1] / shape[1])
d = (shape[0] // res[0], shape[1] // res[1])
grid = np.mgrid[0:res[0]:delta[0],0:res[1]:delta[1]].transpose(1, 2, 0) % 1
# Gradients
angles = 2*np.pi*np.random.rand(res[0]+1, res[1]+1)
gradients = np.dstack((np.cos(angles), np.sin(angles)))
g00 = gradients[0:-1,0:-1].repeat(d[0], 0).repeat(d[1], 1)
g10 = gradients[1:,0:-1].repeat(d[0], 0).repeat(d[1], 1)
g01 = gradients[0:-1,1:].repeat(d[0], 0).repeat(d[1], 1)
g11 = gradients[1:,1:].repeat(d[0], 0).repeat(d[1], 1)
# Ramps
n00 = np.sum(grid * g00, 2)
n10 = np.sum(np.dstack((grid[:,:,0]-1, grid[:,:,1])) * g10, 2)
n01 = np.sum(np.dstack((grid[:,:,0], grid[:,:,1]-1)) * g01, 2)
n11 = np.sum(np.dstack((grid[:,:,0]-1, grid[:,:,1]-1)) * g11, 2)
# Interpolation
t = f(grid)
n0 = n00*(1-t[:,:,0]) + t[:,:,0]*n10
n1 = n01*(1-t[:,:,0]) + t[:,:,0]*n11
return np.sqrt(2)*((1-t[:,:,1])*n0 + t[:,:,1]*n1)
If you are familiar with Perlin noise, nothing should surprise you. Otherwise, I can suggest you to read the first pages of this article which explains Perlin noise very well in my opinion.
An example of what the function generates:
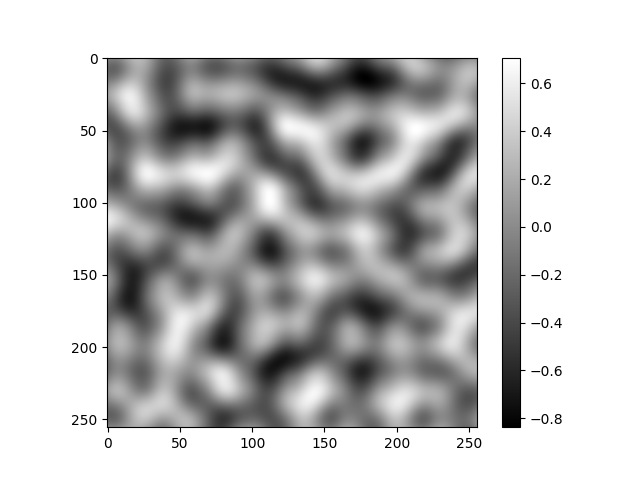
I normalized the gradients so that the noise is always between -1 and 1.
Fractal Image Compression
One year ago, I coded a very simple implementation of fractal image compression for a course and I made the code available on github there.
To my surprise, the repo is quite popular. So I decided to update the code and to write an article to explain the theory and the code.
Non Empty Destructors in C++
Have you already faced problems with nontrivial destructors?
I face one recently which was really annoying. In this article, I want to share with you my knowledge of this problem and the solutions I use to address it.
The Problem
The problem is not really that the destructor is non empty but that the destructor is nontrivial: there is a release of memory or some states are changed in another part of the app.
Let us take a very simple example with a class that does dynamic allocation to explain the problem:
class A
{
public:
A() : mPointer(new int(0))
{
}
~A()
{
delete mPointer;
}
private:
int* mPointer;
}
As we allocate an integer in the constructor, the natural solution for memory management is to free it in the destructor. However, this will have terrible consequences.
For instance, if we do this:
int main()
{
A a;
A anotherA(a);
return 0;
}
A segmentation fault will occur.
Why?
Because when the main function ends, the destructor of A is called to delete a and anotherA. When a is destroyed the memory cell to which the mPointer of a points to is freed. Then, when anotherA is destroyed, we try to free the memory to which the mPointer of anotherA points to. But as anotherA is a copy of a, its mPointer points to the same memory cell as that of a. Thus, we try to free twice the same memory cell which causes the Segmentation fault.
So, the problem is that because of the copy the destructor is called twice on the same attributes.
Note that the copy or move constructors are often called when we use containers. For instance, there is a copy or a move when the std::vector push_back is called.
Tags: cpp
Circular Dependencies in C++
Hi guys, it has been a while since the last post.
I write this short post to tell you about a small script I coded recently. You can find it here on my github account.
Its goal is to draw the “include” dependencies between classes in a C++ project. In particular, it allows to detect circular dependencies very easily or to check the architecture of a project.
You can see the output of the script on a project of mine:

I really like this visual representation which allows to see how classes interact.
However, the true reason why I created this tool is not because I like to see beautiful graphs but because I hate circular dependencies (note that there is none in the graph above). I consider circular dependencies as design flaws. But sometimes in a large project, it could happen that accidentally I create circular dependencies …
Pychain Part 2 - Application: MNIST
In part 1, we have created a fully functional library which is able to create and train neural networks using computational graphs. We used them on very simple examples. Today, we are going to try it on a more serious problem: character recognition.
We are going to use a well-known database in the machine learning and deep learning world named MNIST. The database is available on Yann LeCun’s website. If you have read a bit about neural networks before you should have already seen his name. He is a French scientist who is one of the pioneers of neural networks and inventors of convolutional neural networks and he is now the director of AI at Facebook.
Character recognition is an emblematic problem for two reasons. Firstly, it is one of the first successes and industrial applications of neural networks. It was used since the 90’s to read checks. Secondly, computer vision has always been a leading application domain for neural networks.
In this part, we are going to briefly discover the MNIST database. Then, we are going to train some networks on it and finally, we are going to explore a bit how a neural network works.
